Contents | About | Contact

article 01, issue 01 PDF

Algebraic Determination of Land HPV Velocity

John Snyder
June 21, 2004

Abstract

A method to solve for velocity when power is known.

Introduction

The following equations are intended for exploring how different Human Powered Vehicle (HPV) drag parameters in conjunction with a constant power input influence the velocity result. These calculations depend on several assumptions: a constant rate of travel occurring in a forward linear direction, a zero or positive (uphill) slope, and no wind present .

 

Discussion

The total power required to propel a land HPV at a constant velocity is easily calculated when the sum of losses and gains is also known [reference1]. Solving for velocity posses a slightly greater challenge.

In the equation depicting power due to aerodynamic drag [equation 1], Cd is the aerodynamic drag coefficient, A is the vehicle's reference area, air density is the local current air density, and velocity represents the vehicle's ground speed when traveling through still air.

    [equation 1] 

Because velocity is presented as a number to the third power finding its value, when unknown, requires manipulating a "depressed" cubic equation of the form:

    [equation 2]

The cubic formula was "first published by Girolamo Cardano (1501-1576) in his Algebra book Ars Magna" [reference 2]. By applying several ingenious substitutions and observations Cardano made it possible to solve for velocity by employing the better-known quadratic formula as an intermediate step.


Method

To determine velocity begin by collecting values for the following inputs (S.I. unit): effective drag area, Cd·A (m²); current local air density, air density (kg/m³); combined rider and vehicle mass, mass (kg); local acceleration of gravity, g (m/s²); coefficient of rolling resistance on the local surface, Crr (N/N); roadway slope, slope (radians); input power to drive train, power (watts); and drive train efficiency, efficiency (decimal). 

Perform the following intermediate steps. Conclude by solving for velocity (m/s).


    [equation 3]

    [equation 4]

    [equation 5]

    [equation 6]

    [equation 7]

    [equation 8]





Results



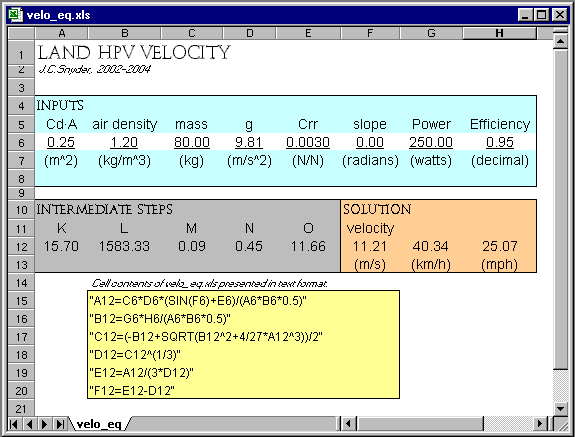
[Illustration]: Screen capture of spreadsheet velo_eq.xls


Concluding Remarks

As presented, this handling allows input only of a non-negative slope value. Notice that the determination of the value of "M" is the adaptation of the quadratic formula to a cubic equation.



References

1. Snyder, John. 2000.CdA and Crr measurement. Human Power.51:9-13

2. Khamsi, Mohamed. Kanust, H. and Marcus, N. 2002. The "Cubic Formula". Math Medics, L.L.C. . Available from URL: http://www.sosmath.com/algebra/factor/fac11/fac11.html 

 

Supplemental Files

Excel format spreadsheets:
velo_eq.xls (Original)
VeloGeschwindigkeitSnyder.xls (German)
VeloGeschwindigkeitsTabelleSnyder.xls (German with multiple rows)


Disclosure Statement

The author is an associate editor of Human Power eJournal.

Contents | About | Contact

Human Power eJournal